Dette er jo sjansen din til å friske opp i trigonometrien fra videregående!

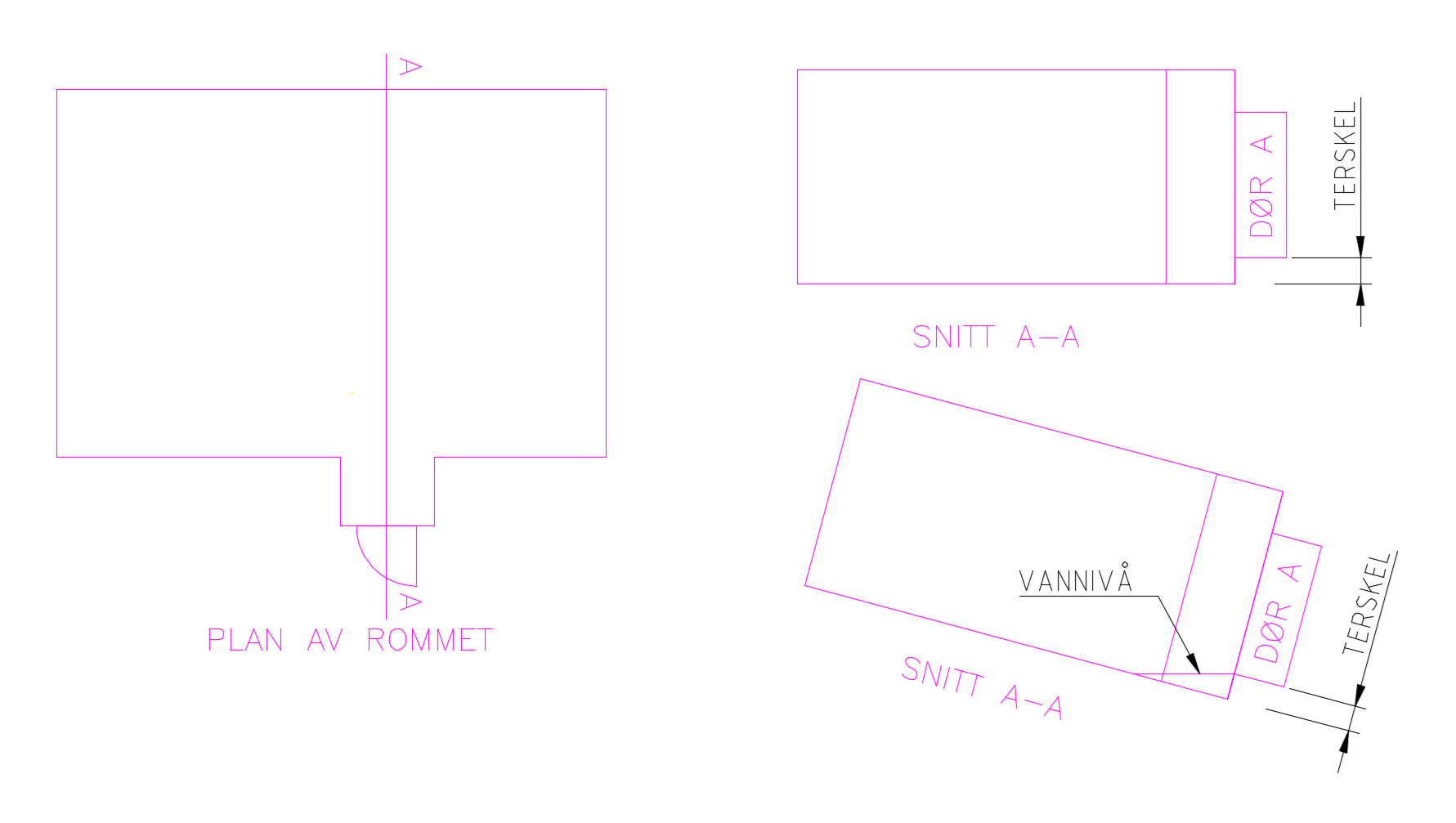
Om du vet bredden på rommet og bredden på døra kan problemet forenkles til at vannet er to vinkelrett-trekantede prismer (en for rommet minus døra og en for selve innhugget til døra, sett fra snitt A-A).

Du vet ikke lengden på sidene til prismet, men du vet høyden av dem, og at en av katetene er terskelhøyden, den andre kateten er terskelhøyden*tan(15deg) , og du vet volumet av summen av prismene (3600 liter). Så lenge du får puslet sammen en formel er det bare å løse for X.

Ikke les videre om du har lyst til å gi det et forsøk selv
Ble inspirert, så jeg prøver:
Bredde rom (minus dør): b
Bredde "innhugg" dør: d
Lengde "innhugg" dør: l
Terskelhøyde t

dørprisme: V1 = d*t^2/2*tan(15)
romprisme: V2 = b*(t/tan(15)-l)*(tan(15)(t/(tan(15)-l)))/2

V1 + V2 = 3600 = b*(t/tan(15)-l)*(tan(15)(t/(tan(15)-l)))/2 + d*t^2/2*tan(15)

Ta overnevnte, skift ut de ukjente med tallene dine og kjør inn i wolframalpha.com

Med veldig stort forbehold om at matten er rett..

EDIT: Formelen over antar at du har samme gulvhøyde i innhugget ditt som resten av rommet. Om terskelen starter i starten av innhugget er utregningen vesentlig enklere..

15 grader var mye. tan(15)=0,27 Dvs, dersom du går 2m horisontalt inn fra døra, så er det 200*0,27=54 cm opp til gulvet. Fartøy som krenger?

Så langt jeg kan se stemmer formelen over, men forutsetter at noe av gulvet lengst fra døra er tørt.

Siste redigering: Friday, October 18, 2019 6:45:35 PM av KjellG

Hei igjen,

Gikk meg over hodet å legge denne inn i wolfram alpha, fikk 220 mm noe som jeg er ganske sikker på at er for lavt. Våger meg på å legge ut dimensjonene på rommet slik at andre kan prøve:
Stemmer forresten at det gjelder et fartøy.

Hei, gjør et forsøk. Rotet selvfølgelig til enhetene mine også. Volumet må selvsagt være i kubikk-millimeter om alle lengdeenhetene er i millimeter..

Det gir deg en terskelhøyde på 220mm som du sier. Kan regne bakover for å sjekke.

Ved å regne tilbake kommer vi frem til at med denne terskelhøyden holder vi 452 liter vann. Whoops.

Riktig svar er forøvrig 721 millimeter.. Vannet er da 2690.8 millimeter inn på gulvet fra døra.

Området foran døra holder da 7.21*26.908*11.0*0.5= 1067 liter
Veggen foran døra har et vannnivå på (2690.8-800)*tan(15) = 506.6mm
Som gir et øvrig vannvolum på 53.0*5.066*(26.908-8.00)*0.5 = 2538 liter

.. summen gir 3605 liter.

EDIT: Hadde jeg vært deg, ville jeg tatt med i beregningen av vann i bevegelse liker å skvulpe, hvis det er viktig at det ikke renner over 

Siste redigering: Monday, October 21, 2019 10:15:50 AM av Svamp

Herlig, det løste problemet mitt og gjorde dagen min, takk skal du ha!

Har du sagt A får du også si B: hva er egentlig dette for problem? Et kjent volum og en kjent krenging??